A well known folk theorem in computer science is that any program can be transformed into a semantically equivalent program of one procedure containing one switch statement inside a while loop. The transformation involves rewriting the program so that each case of the switch is an elementary operation of the original program followed by an assignment to a program counter variable that communicates to the switch statement the next operation to execute. The while loop terminates when the program counter reaches the last operation in the program.
Well in production code nobody will opt for this style, but I think there might be a case where this could come in handy. Few times there is a use case where we have to generate some unique id based on the customer attributes. This could used as slug for pretty urls, pseudo-username etc. Recently I had to write a stored procedure (PL/SQL) in Oracle to generate pseudo-usernames for some million email accounts that we had, with usual rules of length and uniqueness. Instead of writing multiple if-else blocks I came up with something like this.
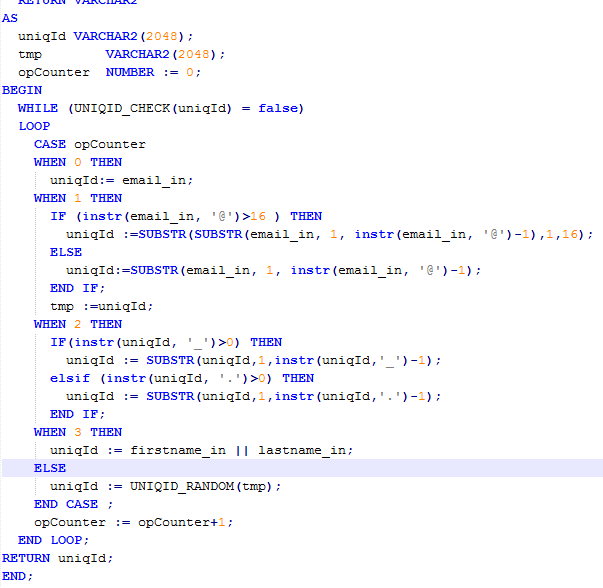
Without making a myriad of if-else nested conditions, I simply wrote a while with condition that checks if pseudo-username generated is within acceptable norms or not. IF yes then program terminates there returning the uniqId created. Else program continues to go on to case statement for next set of steps to generate a psuedo-username. Key thing to note here is that there is a counter maintain which actually determines the which case statement would be picked in each iteration.
Interesting read : This technique has also been used to produce obfuscated C code that produces popular "Twelve Days of Christmas" poem.
Well in production code nobody will opt for this style, but I think there might be a case where this could come in handy. Few times there is a use case where we have to generate some unique id based on the customer attributes. This could used as slug for pretty urls, pseudo-username etc. Recently I had to write a stored procedure (PL/SQL) in Oracle to generate pseudo-usernames for some million email accounts that we had, with usual rules of length and uniqueness. Instead of writing multiple if-else blocks I came up with something like this.

Without making a myriad of if-else nested conditions, I simply wrote a while with condition that checks if pseudo-username generated is within acceptable norms or not. IF yes then program terminates there returning the uniqId created. Else program continues to go on to case statement for next set of steps to generate a psuedo-username. Key thing to note here is that there is a counter maintain which actually determines the which case statement would be picked in each iteration.
Interesting read : This technique has also been used to produce obfuscated C code that produces popular "Twelve Days of Christmas" poem.
Comments
Post a Comment