Skip to main content

Maximum Path Sum

Problem Statement : Starting from top to bottom and moving to adjacent numbers below, find the maximum total for triangle.
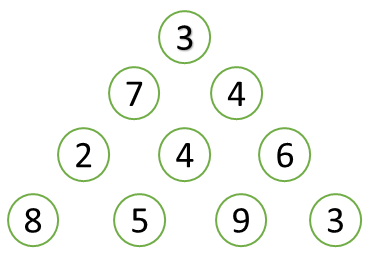
problem

By looking it at the given triangle for few minutes you would see that below is the path having maximum sum i.e. 23.
answer

First approach that may pop in one's mind to solve this problem would be a brute force algorithm. This would be trying every route to find the max sum. The actual number of iterations that will take place for this approach would be 2n, which would be a problem if size of triangle increases.
Bottom to Top Approach
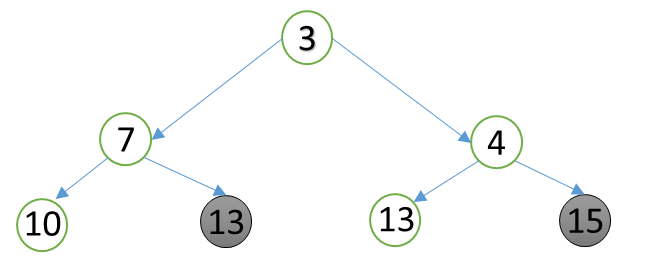
This approach is looking the triangle from bottom to top. First visualize the triangle as follows:
step0
We transform the triangle in sort of tree structure and then only 2 steps need to be repeated until we reach the root node.
Step 1: Choose the max leaf node from the two child leaf nodes.
Step 2: Add the chosen leaf node to the parent node.
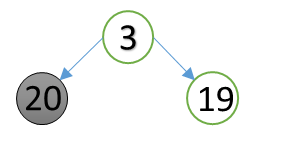
Repeat this until you get to root node. For this triangle this is how it goes, chose the max leaf nodes among the pairs.
step1

Add the chosen nodes to parent.
step2

These steps are repeated until we get to root node.
step3
which gives us 23 the answer.
Labels:

Comments

Post a Comment

Popular posts from this blog

Guide : Spring Boot with Apache CXF for REST services

In this series of guide, we are going to explore writing REST services with Apache CXF using Spring Boot. The project is build using maven. I assume that you already know how to use maven. Step 1 : Adding dependencies for Spring Boot By default you have to inherit the parent pom of spring boot, but that cannot be followed everytime, so I use an alternative to that. I basically add spring boot pom as dependency so that it brings all the dependencies. <properties> <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding> <project.reporting.outputEncoding>UTF-8</project.reporting.outputEncoding> <java.version>1.8</java.version> <spring.version>1.4.3.RELEASE</spring.version> <cxf.version>3.1.10</cxf.version> </properties> <dependencies> <dependency> <!-- Alternative to inheriting from parent spring pom --> <groupId>org.springframework.boot...
7 comments
Read more

Resource Pooling

Requirements for Resource Pool: Allow threads to access resources concurrently Should block threads if no resource is available at the moment Maintain a pool of initialized resources to allow reuse and avoid costly initialization of resources Classes from java.util.concurrent package that will be used: ConcurrentLinkedQueue - An unbounded thread-safe queue. This collection is ideal to act as container of resources since it provides concurrent non blocking access to its elements. Semaphore - Semaphore maintains a set of permits by having a counter. This can be used to acquire or release a permit. If no permits are available then acquire() blocks the invoking thread. Implementation Code reference on github: Resource Pooling
1 comment
Read more

Power of declarative syntax of Lambda

Since Java has introduced lambda, writing code has become a breeze especially when it comes to expressing what you want to computer to do rather than how to do it. The following is a question from Project Euler and is solved using lambdas in Java8. Let d( n ) be defined as the sum of proper divisors of n (numbers less than n which divide evenly into n ). If d( a ) = b and d( b ) = a , where a ≠ b , then a and b are an amicable pair and each of a and b are called amicable numbers. For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220. Evaluate the sum of all the amicable numbers under 10000.  A simple brute force solution is to check every number from 2 to 10000 and if its  an amicable number then add it to sum. Listing it in steps you are basically doing 3 things: Take numbers from 2 to 10000 If number is amicable Add it In Java 7...
2 comments
Read more